Calculate effective subdiffusion time window and parameters from an arbitrary mean square displacement curve.

msd_subdiff(msd, tseq, rel_tol = 0.05, tmax = FALSE, log = FALSE)

Arguments

msd: Vector of sample MSDs.
tseq: Vector of time points at which the MSDs are recorded (see Details).
rel_tol: Relative tolerence for difference between msd and linear fit.
tmax: Logical; if TRUE estimate tmax, otherwise set it to the last MSD timepoint tseq[length(tseq)] (See details).
log: Logical; whether or not the time window is measured on log-scale (See details).

Value

A vector of length 3 if tmax = FALSE, or a vector of length 4 if tmax = TRUE.

Details

Effective subdiffusion time window is defined as the longest time window whose power-law fit is within a small margin of real msd. It is actually performing the linear regression

log(msd[tmin, tmax]) ~ log(D) + alpha * log(tseq[tmin,tmax]).

where tmin is the starting point of time window and tmax is the end of time window. And the relative error between the true msd and power law approximation is defined as

epsilon = max((msd[tmin, tmax] - D * tseq[tmin,tmax]^alpha) / msd[tmin, tmax]).

Since in many experiment tmax is out-of-observation, this function allows to set tmax = tseq[length(tseq)], which is the end of experiment. By doing this we only search for tmin. In addition, the default value of log = FALSE means the length of time window is defined as tmax - tmin, but this doesn't give the best MSD fit on the log-log scale, as there are exponentially more points as we move right in the graph, such that the right side of the graph will dominate the fit. Setting log = TRUE defines the length of time window as log(tmax) - log(tmin). This function finds the longest time window whose epsilon is smaller than rel_tol by applying grid search.

Examples

# simulate a 2D fbm trajectory.
alpha <- 0.8
dt <- 1/60
N <- 1800
acf <- fbm_acf(alpha, dt, N)
dX <- SuperGauss::rnormtz(n = 2, acf = acf)
Xt <- apply(dX, 2, cumsum)

# Compute the MSD of Xt
nlag <- 600
msd <- msd_fit(Xt, nlag = nlag)

plot(dt*(1:nlag), msd, xlab = "Time", ylab = "MSD")


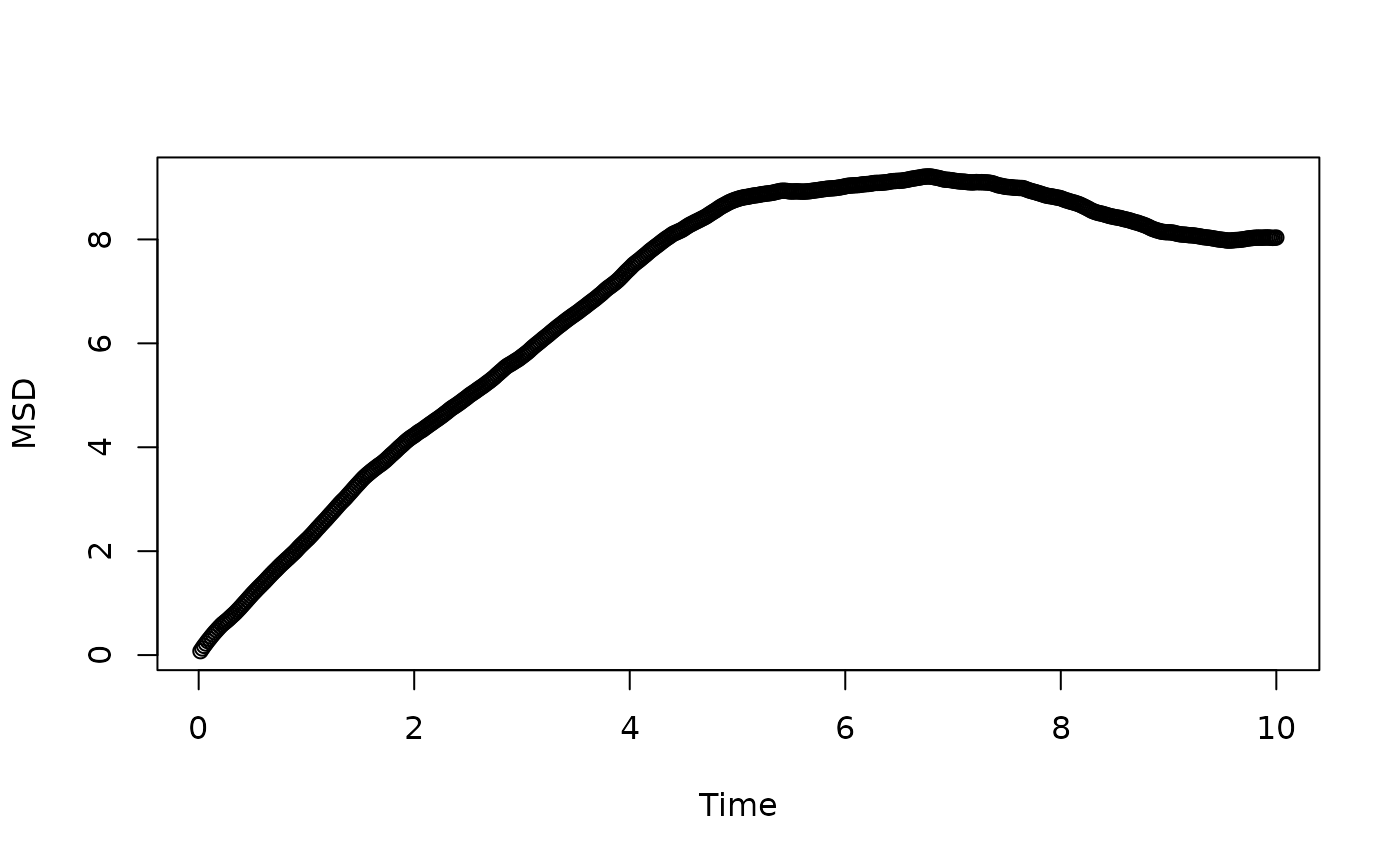# Effective subdiffusion time of MSD
tseq <- 1:nlag * dt
msd_subdiff(msd, tseq)
#>       tmin      alpha          D 
#>  6.0166667 -0.3373696 17.3648079