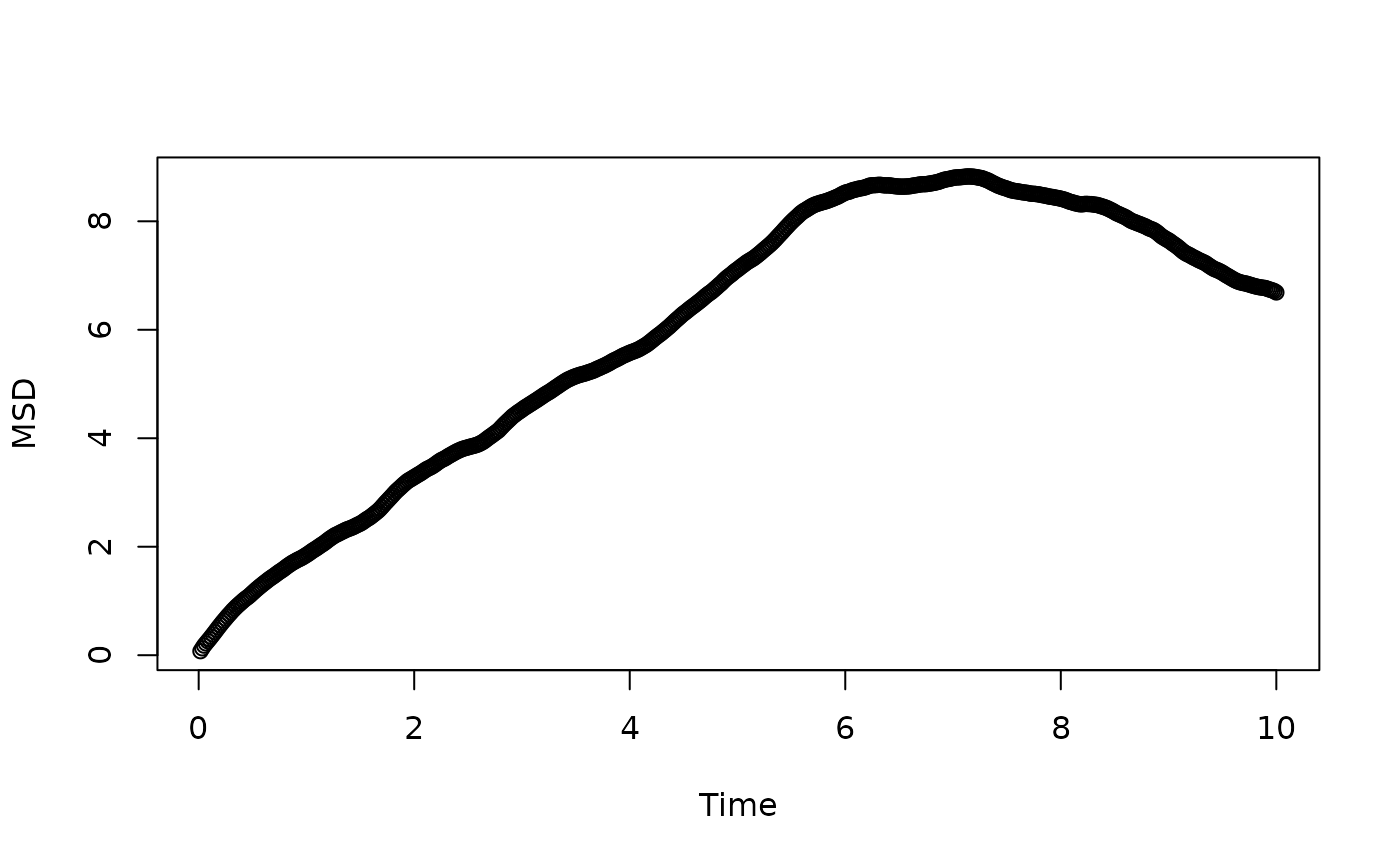
Sample estimate of mean squared displacement.

msd_fit(Xt, nlag, demean = TRUE)

Arguments

Xt: Matrix of trajectory positions, where each row is an observation and each column is a measurement coordinate. The trajectory is assumed to be sampled at a constant frequency.
nlag: Number of MSD lags to calculate.
demean: Logical; whether or not to subtract from Xt a regression-based estimate of its linear drift.

Value

Sample MSD vector of length nlag.

Details

The MSD of a d-dimensional stochastic process X(t) = (X_1(t), ..., X_d(t)) is defined as

MSD_X(t) = E[ (X_1(t) - X_1(0))^2 ] + ... + E[ (X_d(t) - X_d(0))^2 ].

Examples

# simulate a 2D fbm trajectory.
alpha <- 0.8
dt <- 1/60
N <- 1800
acf <- fbm_acf(alpha, dt, N)
dX <- SuperGauss::rnormtz(n = 2, acf = acf)
Xt <- apply(dX, 2, cumsum)

# Compute the MSD of Xt
nlag <- 600
msd <- msd_fit(Xt, nlag = nlag)

plot(dt*(1:nlag), msd, xlab = "Time", ylab = "MSD")